二分探索
二分探索とは
二分探索とはソートされた配列の中から自分が欲しい要素を高速に探し出すアルゴリズムです.
配列を真ん中で2つに割って答えがそれよりも大きいかを判定していき,一回の操作で答えの可能性がある要素を半分に減らしていくため,二分探索と言われています.
例題
ここでは例題を解きながら二分探索を学習していきます.
次のような問題を考えてみます.
例題
要素数Nの配列vが与えられます.
次にQ個のクエリが与えられるので,それぞれのクエリについて出力しなさい.
クエリは整数xで与えられるので,配列vについてx以上の値の中で最も小さい要素を出力しなさい.
ただし,そのような要素が存在しない場合,-1を出力しなさい.
入力
N
v_0 v_1 ... v_N-1
Q
x_0
x_1
...
x_Q-1
制約
N,Q<=2×10^5
v_i,x_i<=10^9
入力はすべて正の整数入力例1
5
1 3 5 7 9
3
3
6
10
出力
3
7
-1入力例2
7
9 3 4 1 7 8 10
5
1
2
3
4
5
出力
1
3
3
4
7これを愚直に実装しようとするとO(NQ)かかり,実行時間がとても大きくなってしまいます.
しかし二分探索というアルゴリズムを用いればO(QlogN)で行うことが可能です.
この問題を次のように考えます.
数が小さい順に並んでいる配列において,答えの下限である右端と上限である左端を決めた時に,右端と左端の真ん中の値は条件に合っているかとは言ってもこれを見ただけでは何のことかさっぱりわからないと思うので,例を挙げながら解説していきます.
二分探索の動き
入力例1の1つ目のクエリ(x=3)を例とします.
問題文より,答えになる値の条件は以下の通りです.
x以上であるこの条件に当てはまる時,その値は答えになる可能性があります.
これを踏まえた上で実際に動きを追ってみましょう.
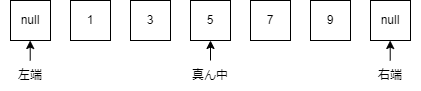
ここでの右端は条件を満たすと分かっている値の中で最小の要素の場所を,左端は条件を満たさないと分かっているものの中で最大の要素の場所を指しています.
始めは,右端,左端ともに分かっている値が無いので,左端は配列の左外(-1の場所)に,右端は配列の右外(Nの場所)に設定しておきます.
今回の一行目のクエリではx=3であり,この時真ん中の値である5は条件に当てはまる(x以上)なので,答えは少なくとも5よりも右側には存在しないことが分かります.
なので, 答えの上限である右端を真ん中まで持っていきます.
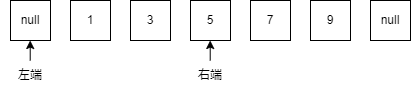
次にまた真ん中の値を見ます.
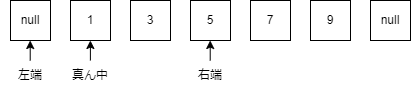
今回の真ん中の値である1は条件に当てはまらない(x以上ではない)ことから,答えは1から左には存在しないことが分かるので,左端を真ん中まで持っていきます.

この操作を右端と左端の位置の差が1になる(真ん中を選べなくなる)まで繰り返します.
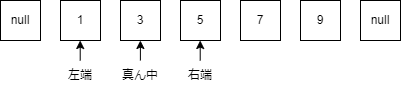
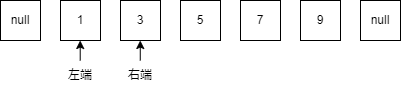
右端と左端の位置の差が1(真ん中が選べない状態)になったので探索を終了します.
この時の右端が答えを満たす最小の数,左端が答えを満たさない最大の数になります.
よって一つ目のクエリの答えは3です.
二つ目のクエリ(x=6)でも動きを見てみましょう.

この時,真ん中の値である5は条件に当てはまらないので, 左端を真ん中まで持っていきます.
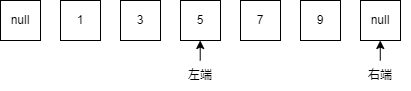

7は条件に当てはまるので,右端を真ん中に持っていきます.

ここで右端の位置と左端の位置の差が1になったので探索を終了します.
この時点での右端がさしている場所の要素が答えとなるので,答えは7になります.
ここまでの流れを整理してみます.
配列を小さい順にソートする.
答えとなる条件式を立てる.
右端と左端を設定する.
真ん中の値が条件式に当てはまるかどうかを確認する.
もし当てはまれば右端を真ん中の位置に,当てはまらなければ左端を真ん中の位置に持ってくる.
4,5の操作を右端と左端の位置の差が1になるまで繰り返す.
実装
これらを踏まえたうえで,ここからは実際に実装してみます.
#include<bits/stdc++.h>
using namespace std;
int main(){
//以下標準入力
int N;
cin>>N;
vector<int> v(N);
for(int i=0;i<N;i++){
cin>>v[i];
}
int Q;
cin>>Q;
vector<int> x(Q);
for(int i=0;i<Q;i++){
cin>>x[i];
}
//ここまで
return 0;
}さっきの流れに沿って実装していきます.
- 配列を小さい順にソートする.
ソートはstd::sortを使うことで行うことができます.
sort(v.begin(),v.end()); //1. 配列を小さい順にソートする- 答えとなる条件式を立てる.
条件式は正しいかどうかをboolで返すとよいので,次のような判定用の関数を宣言します.
//2. 条件式を立てる
// aがx以上ならばtrueを返す
bool isok(int x,int a){
return a>=x;
}今回の場合はx以上であれば答えになる可能性があるのでこのような関数にしましたが,二分探索の条件が必ずしもこのような条件であるとは限らないので,その場に応じた条件式を自分で立てて,この関数の中に書いてください.
- 右端と左端を設定する.
今回は右端をright,左端をleftとしています.
また,ついでに真ん中の位置を記憶しておく変数もmidとして宣言しておきます.
sort(v.begin(),v.end()); //1. 配列を小さい順にソートする
int right=N,left=-1,mid; //3. 右端と左端を設定する右端の初期値は-1,左端の初期値は配列の大きさ(今回の場合はN)にしてください.
- 真ん中の値が条件式に当てはまるかどうかを確認する.
真ん中の位置は右端と左端の平均をとるとわかります.
また,条件式に当てはまるかどうかはさっき宣言した条件式の返り値を見るとわかります.
sort(v.begin(),v.end()); //1. 配列を小さい順にソートする
int right=N,left=-1,mid; //3. 右端と左端を設定する
//4. 真ん中の値が条件式に当てはまるかどうかを確認する.
mid=(left+right)/2;
if(isok(x[i],v[mid])){ //もし真ん中の値(v[mid])が条件式に当てはまるならば
}
else{ //当てはまらなければ
}- もし当てはまれば右端を真ん中の位置に,当てはまらなければ左端を真ん中の位置に持ってくる.
leftやrightにmidを代入します.
sort(v.begin(),v.end()); //1. 配列を小さい順にソートする
int right=N,left=-1,mid; //3. 右端と左端を設定する
//4. 真ん中の値が条件式に当てはまるかどうかを確認する.
mid=(left+right)/2;
if(isok(x[i],v[mid])){ //もし真ん中の値(v[mid])が条件式に当てはまるならば
right=mid;//5. 右端を真ん中の位置に持ってくる
}
else{ //当てはまらなければ
left=mid;//5.左端を真ん中の位置に持ってくる
}- 4,5の操作を右端と左端の位置の差が1になるまで繰り返す.
4と5の部分をfor文やwhile文で条件を満たすまでループさせます.
sort(v.begin(),v.end()); //1. 配列を小さい順にソートする
int right=N,left=-1,mid; //3. 右端と左端を設定する
while((right-left)>1){ //6. 4,5の操作を右端と左端の位置の差が1になるまで繰り返す.
//4. 真ん中の値が条件式に当てはまるかどうかを確認する.
mid=(left+right)/2;
if(isok(x[i],v[mid])){ //もし真ん中の値(v[mid])が条件式に当てはまるならば
right=mid;//5. 右端を真ん中の位置に持ってくる
}
else{ //当てはまらなければ
left=mid;;//5.左端を真ん中の位置に持ってくる
}
}これで二分探索の実装ができました.
ループを抜けたときのrightの位置が条件を満たす最小の値で,leftの値が条件を満たさない最大の値です.
最後に今回の例題の実装例です.
#include<bits/stdc++.h>
using namespace std;
//2. 条件式を立てる
// aがx以上ならばtrueを返す
bool isok(int x,int a){
return a>=x;
}
int main(){
//以下標準入力
int N;
cin>>N;
vector<int> v(N);
for(int i=0;i<N;i++){
cin>>v[i];
}
int Q;
cin>>Q;
vector<int> x(Q);
for(int i=0;i<Q;i++){
cin>>x[i];
}
//ここまで
//以下二分探索の実装
sort(v.begin(),v.end()); //1. 配列を小さい順にソートする
for(int i=0;i<Q;i++){ //入力の数だけ繰り返す
int right=N,left=-1,mid; //3. 右端と左端を設定する
while((right-left)>1){ //6. 4,5の操作を右端と左端の位置の差が1になるまで繰り返す.
//4. 真ん中の値が条件式に当てはまるかどうかを確認する.
mid=(left+right)/2;
if(isok(x[i],v[mid])){ //もし真ん中の値(v[mid])が条件式に当てはまるならば
right=mid;//5. 右端を真ん中の位置に持ってくる
}
else{ //当てはまらなければ
left=mid;//5.左端を真ん中の位置に持ってくる
}
}
if(right==N){ // 条件を満たすものがなかった時
cout<<-1<<endl;
}
else{
cout<<v[right]<<endl; //答えを出力
}
}
return 0;
}