累積和
はじめに
次のような問題を考えてみます.
問題
長さNの配列AとQ個のクエリが与えられます.
それぞれのクエリについての答えを出力してください.
クエリの内容
整数L,Rが与えられるので,配列AのL番目からR番目までの要素の総和を求めてください.
入力
N Q
A_0 A_1 ・・・ A_N-1
L_0 R_0
L_1 R_1
.
.
.
L_Q-1 R_Q-1
制約
1<=N,Q<=2×10^5
1<=A_i<=1000
1<=L<=R<=N入力例
10 3
5 2 3 1 4 7 1 2 5 5
2 9
3 6
1 10出力例
25
15
35この問題の入力例を考えてみます.
愚直にやろうとすれば2+3+1+4+7+1+2+5とすべて足していって答えを出すと思いますが,この方法だと計算量がO(N)となります.
与えられた範囲が1つだけの場合はこの愚直解でも通せますが,今回の問題のように何回も範囲が与えられる場合は計算量はO(NQ)となってしまい,大きくなってしまいます.
そこで使えるのが累積和です.
累積和の考え方
累積和とは,事前に配列の総和をO(N)で計算しておくことで,指定範囲内の配列の要素の総和をO(1)で処理できるアルゴリズムです.
何回も範囲の総和を求めるときに使えます.
前計算
まずは前計算として要素数N+1の新しい配列宣言し(ここでは新しく宣言した配列をCとします),C_iにはAの前から1番目からi番目までの総和を格納します. ただし,Aの前から0番目には0が格納されていると仮定してC_0には0を格納しておきます.
例を出して説明すると,C_1にはA_0までの総和(A_0),C_2にはA_1までの総和(A_0+A_1),C_3にはA_2までの総和(A_0+A_1+A_2),C_4にはA_3までの総和(A_0+A_1+A_2+A_3)格納されているといった感じです.
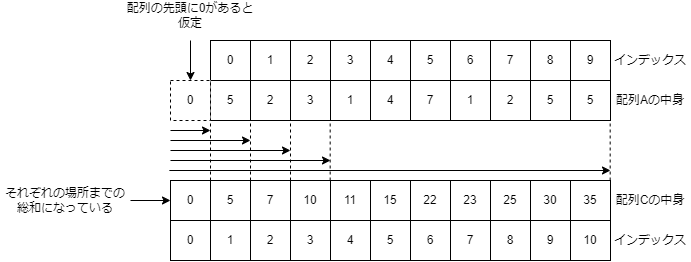
そして,i番目までの総和にi+1番目の要素を足すとi+1番目までの総和になることから,C_iにA_iを足すだけでC_(i+1)が求められます.
例えばC_3(A_0+A_1+A_2)がわかっている場合,それにA_3を足すとC_4が求められます.
よって,C_(i+1)をそれぞれO(1)で求められるので,この前計算はO(N)で求められます.
実装例(前計算の部分だけ)
vector<int> C(N+1);
C[0]=0;//C_0は0
for(int i=0;i<N;i++){
C[i+1]=C[i]+A[i];//C_i(A_(i-1)までの総和)にA_iを足して求める
}これで前計算は終わりです.次は実際に範囲の総和を求めてみましょう.
範囲の総和
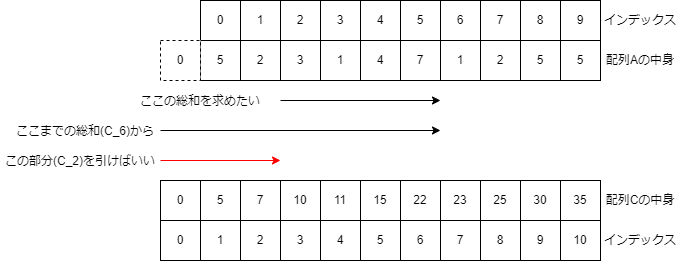
[L,R]の範囲の総和を求めるときは C_R - C_(L-1) で求められます.
簡単に言うと,Aの前からL番目からR番目の総和を求めるには,AのR番目までの総和から余分に足されている分のL-1番目までの総和を引くことで求められます.
例題の2つ目のクエリである[3,6]を例として考えてみます.
[3,6]の範囲の総和は A_2 + A_3 + A_4 + A_5 で求められます.
ここでC_6を見てみましょう. C_6はA_5までの総和でした.なので C_6 = A_0 + A_1 + A_2 + A_3 + A_4 + A_5 です.
今回欲しいのは A_2 + A_3 + A_4 + A_5 なので,A_0 + A_1 が邪魔です.なのでこの部分を引いてあげます.A_0 + A_1 はAの前から2番目までの総和なので,A_0 + A_1 = C_2です.
よって C_6 - C_2 で求められます.
最後に例題の実装例です.
#include<iostream>
#include<vector>
using namespace std;
int main(){
int N,Q;
cin>>N>>Q;
vector<int> A(N);
for(int i=0;i<N;i++){
cin>>A[i];
}
//前計算
vector<int> C(N+1);
C[0]=0;//C_0は0
for(int i=0;i<N;i++){
C[i+1]=C[i]+A[i];//C_i(A_(i-1)までの総和)にA_iを足して求める
}
int L,R;
for(int i=0;i<Q;i++){
cin>>L>>R;
cout<<C[R]-C[L-1]<<endl;//範囲の総和を求める
}
return 0;
}